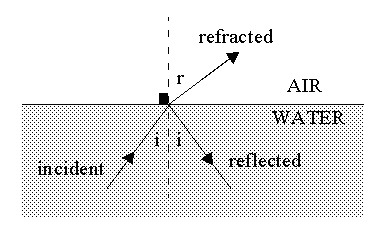
The intensity of the reflected beam relative to that of the incident beam (the "reflectance"), again depends on the angle of incidence and the direction of polarization of the light, as shown below.
As in the case of rare-to-dense, or external, reflection (see previous article), a ray of light that propagates through water and is incident on an air/water interface will also be partially refracted and partially reflected. In this case (a dense-to-rare effect) it is termed internal reflection.

The intensity of the reflected beam relative to that of the incident beam (the "reflectance"), again depends on the angle of incidence and the direction of polarization of the light, as shown below.
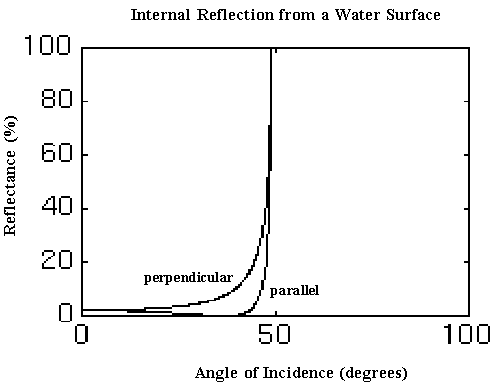
which in this case is 37 degrees. Note that both curves approach 100% as the angle of incidence approaches the critical angle of 48.8 degrees (when r=90 degrees) and that for angles greater than this there is no refracted beam. This is known as total internal reflection (see the article).
REFERENCES: .
J. D. Jackson, "Classical Electrodynamics" (John Wiley and Sons 1962), Vol. 1, Chapter 7.
F. A. Jenkins and H. E. White, "Fundamentals of Optics" (McGraw-Hill 1957), Chapter 25.