Total Internal Reflection

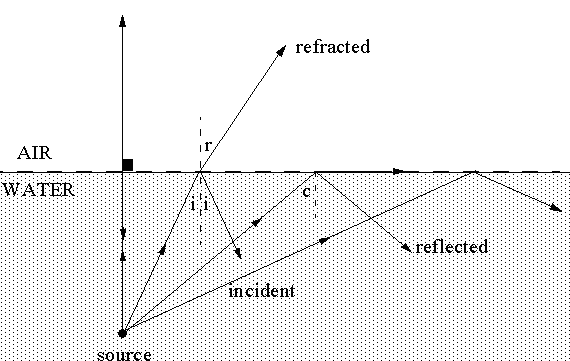
Suppose that a ray of light originates from an underwater source and travels upwards. At the surface part of it will be refracted into air and part will be reflected back into the water. The angle of reflection equals the angle of incidence, as shown, while the angle of refraction must be consistent with Snell's law: 

n(w)sin(i) = n(a)sin(r)                  Equation 1

where n(w) and n(a) are the indices of refraction of water and air respectively. With n(w)=1.33 and n(a)=1.00 we have

sin(r) = (1.33)sin(i)                    Equation 2

At normal incidence (i=0 degrees) the transmitted ray is undeviated and the reflected ray travels directly back to the source. Increasing the angle of incidence, i.e. making the ray meet the water surface more obliquely, causes the refracted ray to bend more towards the surface. This continues until the angle of refraction reaches its maximum value of 90 degrees, corresponding to the critical angle of incidence 'c' given by the equation (1.33)sin(c)=1, or c=48.8 degrees. For angles of incidence greater than the critical angle there is total internal reflection.





This does not mean that on the air side of the surface the wave amplitude suddenly drops to zero at the critical angle. Electromagnetic theory predicts (and measurements confirm) that for i > c there is in fact an electromagnetic disturbance that propagates parallel to the surface and dies off exponentially in a direction normal to the surface. The energy it carries oscillates back and forth across the surface but there is no net transfer of energy across the surface. The penetration distance into the air is extremely small, being only a few wave lengths, and decreases rapidly with an increase in the angle of incidence. For example, when i = 55 degrees the wave amplitude drops by a factor of 1/5000 over a distance of three wave lengths. For i=65 degrees the corresponding factor is approximately 3/1000000.

REFERENCE:

J. D. Jackson, "Classical Electrodynamics" (John Wiley and Sons 1962), Vol. 1, Chapter 7.