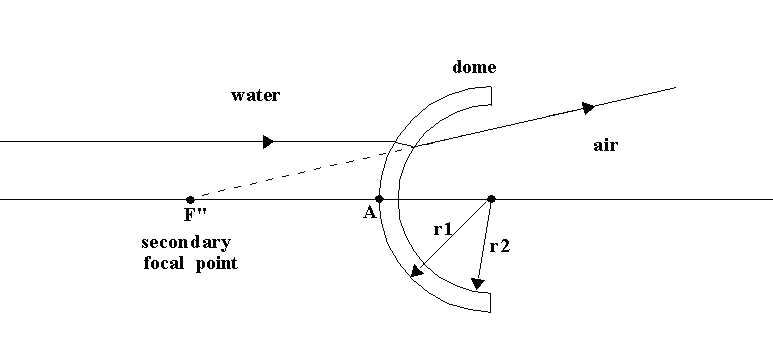

AF" = -r2*[n"/(1-n)]*(1-g)/[1 - g/(1-n)] - (r1-r2) Equation 1
where
g = [(n'-n)/n']*(r1-r2)/r1
n = index of refraction of water
n' = index of refraction of the dome material
n" = index of refraction of air
Putting n"=1 and n=4/3 (this is accurate enough for our purposes), get
AF" = 3*r2*(1-g)/(1+3g) - (r1-r2) Equation 2
with
g = [1 - 4/(3n')]*(r1-r2)/r1
Typically, the value of g is of the order 1/100, so we can write, to an excellent approximation (error = .03%)
AF" = 3*r2*(1-4g) - (r1-r2) Equation 3
Equations 1 and 2 are exact, and Equation 3 is nearly exact, but neither can serve as a simple rule of thumb for locating the infinity virtual image. To find a simple
rule we must make a few simplifications. First, we note that the dome's index of refraction is typically in the range 1.5 < n' < 1.6, and over this range the right hand
side of Equation 3 is a weak function of n'. So, accuracy will not suffer much by putting n'=3/2. Next, express r1 and r2 in terms of the mean dome radius
R=(r1 + r2)/2 and the dome thickness t = r1 - r2:
r1 = R + t/2
r2 = R - t/2
Substituting for n', r1, and r2 in Equation 3, expanding in powers of the small quantity t/R, and keeping only the zeroth-order terms, we get
AF" = 3R - 4t + 5t/18 Equation 4
or, since the 3rd term is small compared to the 2nd term, the very simple result
AF" = 3R - 4t Equation 5
The table shown below compares the results from Equation 2 (exact), Equation 3 (almost exact), and Equation 5 (rule-of-thumb) for several dome indices of refraction and dome radii. All distances are given in inches. Note that the rule-of-thumb formula is usually accurate to within one or two tenths of an inch!!
The rule-of-thumb for locating the infinity virtual image is therefore: " three radii minus four thicknesses from the front of the dome"
DOME TO VIRTUAL IMAGE
------------------------
almost rule
exact exact of
n' r1 r2 t (Eq.1) (Eq.2) thumb
------------------------
1.50 2.500 2.375 .125 6.84 6.84 6.81
2.250 .250 6.21 6.20 6.13
2.125 .375 5.60 5.57 5.44
2.000 .500 5.00 4.97 4.75
3.000 2.875 .125 8.34 8.34 8.31
2.750 .250 7.70 7.69 7.63
2.625 .375 7.08 7.06 6.94
2.500 .500 6.47 6.44 6.25
3.500 3.375 .125 9.84 9.84 9.81
3.250 .250 9.20 9.19 9.13
3.125 .375 8.57 8.55 8.44
3.000 .500 7.95 7.93 7.75
4.000 3.875 .125 11.34 11.34 11.31
3.750 .250 10.69 10.69 10.63
3.625 .375 10.06 10.05 9.94
3.500 .500 9.44 9.42 9.25
1.55 2.500 2.375 .125 6.80 6.80 6.81
2.250 .250 6.14 6.12 6.13
2.125 .375 5.50 5.47 5.44
2.000 .500 4.88 4.83 4.75
3.000 2.875 .125 8.30 8.30 8.31
2.750 .250 7.63 7.62 7.63
2.625 .375 6.98 6.95 6.94
2.500 .500 6.35 6.30 6.25
3.500 3.375 .125 9.80 9.80 9.81
3.250 .250 9.12 9.11 9.13
3.125 .375 8.46 8.44 8.44
3.000 .500 7.82 7.78 7.75
4.000 3.875 .125 11.30 11.30 11.31
3.750 .250 10.62 10.61 10.63
3.625 .375 9.95 9.93 9.94
3.500 .500 9.30 9.27 9.25
1.60 2.500 2.375 .125 6.77 6.76 6.81
2.250 .250 6.07 6.05 6.13
2.125 .375 5.41 5.36 5.44
2.000 .500 4.77 4.70 4.75
3.000 2.875 .125 8.27 8.26 8.31
2.750 .250 7.56 7.54 7.63
2.625 .375 6.88 6.84 6.94
2.500 .500 6.23 6.17 6.25
3.500 3.375 .125 9.76 9.76 9.81
3.250 .250 9.05 9.04 9.13
3.125 .375 8.36 8.33 8.44
3.000 .500 7.70 7.64 7.75
4.000 3.875 .125 11.26 11.26 11.31
3.750 .250 10.55 10.53 10.63
3.625 .375 9.85 9.82 9.94
3.500 .500 9.18 9.13 9.25