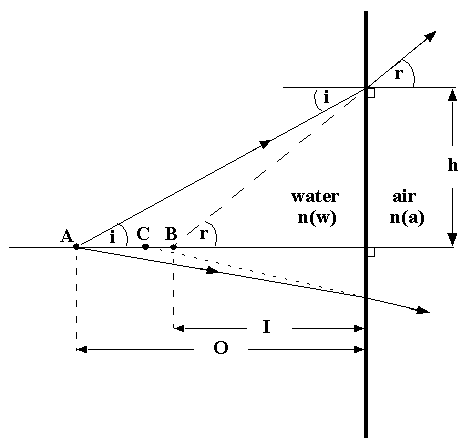
In-water objects viewed through a planar air/water interface, such as a mask or flat port of a camera housing, appear closer than they really are. This is due to refraction at the interface, and because the index of refraction of water is greater than that of air. Consider a point object at A, which is a perpendicular distance O from the interface, and a light ray from A incident on the interface at angle 'i', intersecting it at a height 'h' . If the indices of refraction of water and air are n(w) and n(a), respectively, the angle of refraction 'r' is given by Snell's law:
sin(i)/sin(r) = n(a)/n(w) (Equation 1)
I = O*tan(i)/tan(r) (Equation 2)

The magnitude of I clearly depends on the angle 'i'. By combining Equations 1 and 2, we get
I = O*[n(a)/n(w)]*cos(r)/cos(i) (Equation 3)
and by solving for cos(r) from Equation 1 and substituting into Equation 3, we find that a decrease in 'i' produces an increase in I (see the lower ray in the figure). In fact, as 'i' becomes very small, the virtual object point approaches C, for which
I = O*n(a)/n(w) (Equation 4)
Using the values n(a)=1.0 and n(w)=1.33, we thus have the approximation: I=0.75*O . Since the angle of view subtended at the human eye is relatively small, Equation 4 is applicable, and the eye therefore sees underwater objects as being approximately 25% closer than measured. Equation 3 explains just one of the aberrations produced by a plane port: light rays coming from the same point on an object, but travelling in very different directions, will appear to be coming from virtual object points at slightly different distances in front of the port. If a conventional 'uncorrected' lens having either a wide field of view or used with a large aperture (or both) is placed behind a plane port, the image produced at the film plane will be blurred. And the blurring gets worse as the object is brought closer.
REFERENCE: