Particle Motion in Deep Water

The small amplitude theory of surface water waves lends itself to a classification of waves based on the relative depth d/L, where d is the water depth and L is the wave length. Waves for which d/L > .5 are referred to as deep water waves. Studies of water particle motions associated with such waves show that, aside from a very small forward displacement (mass transport), the particles beneath a wave essentially move in circular orbits. At the surface the orbit radii are equal in magnitude to the wave amplitude, while for deeper particles the radii decrease exponentially with their distance below the still water surface level (see the figure below).

Designating this distance by 'z', the orbit radii are given by

So, if we know the wave's length and amplitude, we should be able to use Equation 1 to determine how deep we can 'feel' a surface disturbance.

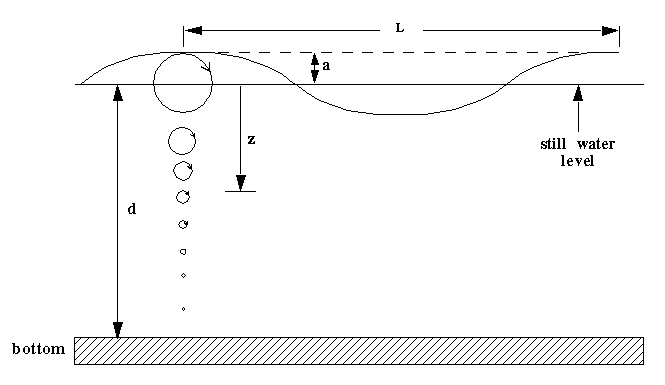
The wave length of a deep-water wave depends only on its period T and the acceleration due to gravity g:

The wave period is simply the time between consecutive wave crests as they pass a fixed point. All deep-water waves with the same period, regardless of actual depth, have the same wave length.

Let's see what happens for 2-foot waves (a=1 foot) with various periods. In particular, let's see how deep you must go before the orbit radii of small bits of floating debris become smaller than 1 inch, which implies an overall particle displacement of less than 2 inches. The results are presented in the following table.

For example, 2 foot waves 3 seconds apart produce a 2-inch particle displacent at 23 feet below the surface. As is clear from Equation 1, the longer the wave length the less rapid the vertical attenuation of the surface disturbances.

REFERENCES:

Robert M. Sorensen, "Basic Wave Mechanics for Coastal and Ocean Engineers" (John Wiley & Sons, 1993), Chapter 2..

Last Modified: 11:15pm , May 06, 1997