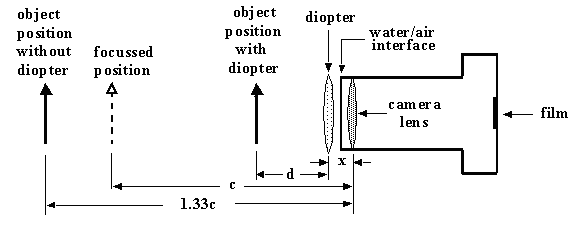
Underwater close-up photography with a submersible camera is usually accomplished by the use of extension tubes or add-on positive diopter lenses. An extension tube causes a decrease in the lens-to-subject distance, and a corresponding increase in the magnification ratio, by increasing the lens-to-film distance. A diopter achieves the same results by producing a lens combination with a shorter effective focal length. Either approach renders the distances on the camera lens' focussing ring useless, which is why the best (and most expensive) tube/diopter setups are provided with framers for outlining the effective field-of-view and for positioning the subject. It is possible, however, to use inexpensive off-the-shelf diopters, provided that one either develops a "feel" for the appropriate lens-to-subject distance or builds a framer. It is best, of course, to assemble the configuration and perform actual in-water tests. But it helps to have some quantitative understanding of diopter optics before proceeding.

where f(w) is the diopter's in-water focal length and 'x' is the distance between the diopter and the camera lens. Note that 'd' does not depend on the focal length of the camera, but only on the focussing distance. When the lens is focussed on infinity we get d=f. That's because rays from an object situated at a lens' focal point will emerge from the lens parallel, as if they had come from infinity. So, an easy rule of thumb is that with focus on infinity and with a +D diopter lens, the subject must be 1/D meters away (+D must be the effective in-water lens power, see "Diopter Focal Lengths and Powers").
For example, consider two diopters with in-air powers of +4 diopters and +10 diopters, and each having index of refraction 1.6. The following table shows their effective in-water focal lengths and the subject distances corresponding to the infinity-focus and minimum-focus settings of the standard Nikonos-V lens, the 35 mm W-Nikkor. For typical values of x, the subject distance is a weak function of x, so we assume that x=0.
+4 diopter +10 diopter in-air focal length 0.25 m 0.10 m in-water focal length 0.75 m 0.30 m subject distance for infinity focus 0.75 m 0.30 m subject distance for 0.8m focus 0.44 m 0.23 m