Not quite. Refraction at a planar water-air interface (such as due to a mask faceplate) produces an image that seems larger than the corresponding object, but the degree of magnification depends on both the object-to-faceplate and eye-to-faceplate distances. If the index of refraction of the water is n(w)=1.33 and that of air is n(a)=1.00, the factor 1.33 is the maximum possible magnification that can be produced by a planar water-air interface.

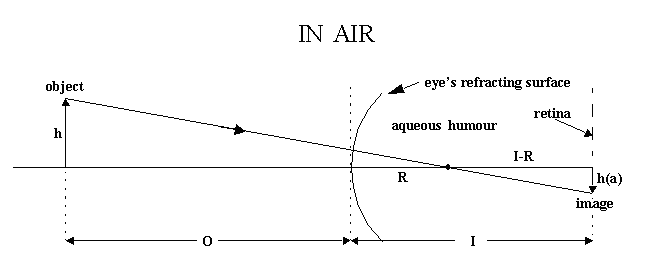
By similar triangles, the height of the retinal image is
h(a) = h(I-R)/(O+R) Equation 1
For the same relative positions of object and eye, but with the object in water and the eye in air behind a water-air interface, the configuration is as shown below. Note the refraction at the faceplate, with angle of incidence 'i' and angle of refraction 'r', and the magnified retinal image.
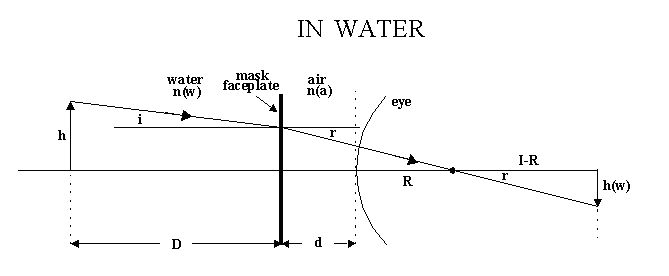
The image height is now
h(w)=(I-R)tan(r) Equation 2
Again using similar triangles, the object height can be expressed as
h = Dtan(i) + (d+R)tan(r) Equation 3
Substituting this expression for h into Equation 1, and then using Equation 2, we get the ratio
h(w)/h(a) = (O+R)/[Dtan(i)/tan(r) + (d+R)] Equation 4
But the refraction at the faceplate is described mathematically by Snell's Law, i.e.
sin(i)/sin(r) = n(a)/n(w) Equation 5
and for small angles at the eye (paraxial rays) we know that the sines and tangents of angles are approximately the same, so we can assume that
tan(i)/tan(r) = n(a)/n(w) Equation 6
Substituting this into Equation 4 and noting that O=D+d, we get the retinal image magnification
M = h(w)/h(a) = (D+d+R)/[Dn(a)/n(w) + (d+R)] Equation 7
or, in the more instructive form,
M =m{[ (1+ (d+R)/D]/[1+m(d+R)/D]} Equation 8
where
m = n(w)/n(a) = 1.33 Equation 9
It is now clear that the magnification M due to the water-air interface is always LESS than 1.33. M approaches this value only in the limit as the distance D (object to mask) approaches infinity, or when both d and R approach zero. The following table gives some representative values of M for typical values of D and d, with R=0.8 cm
object to eye to
faceplate faceplate
D (cm) d (cm) M
-----------------------------
200 0 1.328
100 0 1.327
50 0 1.323
200 2.5 1.323
100 2.5 1.316
50 2.5 1.303
25 2.5 1.281
100 5.0 1.306
50 5.0 1.286
25 5.0 1.252
As the object approaches the faceplate and/or the eye recedes from it, the magnification decreases. At an object distance of 25 cm with the eye 2.5 cm behind the faceplate, the image is only 28% larger.
The foregoing dealt strictly with the size of the retinal image. How the brain perceives that image depends on many other factors. Studies have shown (Ross et al), that the brain adapts rather quickly to the underwater environment, so that initial errors in judging object sizes are significantly reduced during the course of a dive. Moreover, size judgments improve with diving experience.
REFERENCES:
H. E. Ross, S. S. Franklin, G. Weltman, and P. Lennie, 'Adaptation of Divers to Size Distortion Under Water', Br. J. Psychol. (1970), 61, pp. 365-373.